Sean a y b dos enteros positivos tales que sus raices cuadradas no son racionales. ¿En qué casos es racional?
- Comentarios
- Rebloguear
-
Suscribirse
Suscrito
¿Ya tienes una cuenta de WordPress.com? Inicia sesión.
Si esa resta es un número racional podíamos llegar a la siguiente igualdad:
de donde se sigue (dividiendo entre p/q solo si es distinto a cero):
lo cual contradice la hipótesis de que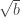 es irracional.
es irracional.
por lo tanto la resta original es racional solo cuando es cero
¿puede ser racional?
ser racional?
si raiz de p mas raiz de q con p y q primos es irracional… cómo lo demuestro?
el truco usual con sumas de raices es multiplicar por la conjugada, o sea:
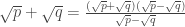
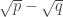 es irracional (es lo demostrado arriba en el primer comentario)
es irracional (es lo demostrado arriba en el primer comentario)
$=latex \frac{p-q}{\sqrt{p}-\sqrt{q} }$
como estamos suponiendo que p y q son distintos, entonces
si dice que p y q son distintos por que p y q no pueden ser primos
no necesariamente son primos, pero si son primos relativos, es en el supuesto de que tengamos un número racional p/q
q numeros son irracionales ?
los numeros irracionales son los decimales no periodicos ni exactos