Una de las cosas mas importantes en matemáticas es el principio de inducción. Sea una propiedad de algunos números de modo que ésta propiedad se «contagie» de un número al siguiente. Si el cero cumple esta propiedad, entonces todos los naturales cumplen.
Puesto como formula…
un buen ejercicio que requiere inducción es el siguiente:
Encontrar todas las funciones de números naturales que cumplen con que
Pero hay un hecho equivalente en los números naturales, se le llama el principio del buen orden:
Cualquiér subconjunto de los números naturales tiene un mínimo.
Para ilustrar aquí está la demostración de una implicación:
Supongamos que cualquier conjunto de naturales tienen un mínimo, entonces el siguiente conjunto tiene un mínimo:
llamemos a ese mínimo. si
no es cero, entonces
y se cumple
, por lo tanto
contradicción! (m es el primero que no cumple).
El principio del buen orden se usa mucho con otra técnica llamada descenso infinito. A veces para encontrar si existe o no un objeto suponemos que hay alguno de tamaño n y lo transformamos para encontrar otro de tamaño menor, a esa técnica se le llama descenso infinito, es muy usada para demostrar por contradicción, p.ej
Encontrar las soluciones enteras de

para resolverlo primero hay que ver cuáles son las congruencias de un cuadrado módulo 7:
1, 4, 2, 2, 2, 4, 1, 0
Es fácil notar aqui que ninguna suma de dos residuos es cero, mas que cuando ambos son cero, o sea si ambos son divisibles por 7. En ese caso se pueden escribir como y
y nos queda la siguiente ecuación:
que es equivalente a
pero en esta ultima y
son menores… Entonces si hubiera una solución entera distinta de cero, podríamos encontrar otra menor (eso contradice el principio del buen orden)
Un buen ejercicio con inducción es demostrar que los números de Fibonacci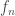 cumplen con la siguiente fórmula:
cumplen con la siguiente fórmula:
donde es la raíz mayor de la ecuación
es la raíz mayor de la ecuación
